Until this moment multiple concepts related to topological quantum computation have been covered on this blog. Notably, we simulated basic Majorana Zero Modes physics in 1D topology, then we performed topological braids to convert the ground state into the ground state of different topological phase, we defines and simulated topological qubits and applied them to simulate quantum teleportation.

The idea of the topological gap has been briefly mentioned and came up as a source of topological protection. One of the characteristics of the topological regime is the degeneracy of the ground state. This degeneracy gets broken during the topological phase transition as the system enters the trivial regime. We have already covered and simulated those phase transitions both adiabatically and using unitary braids, however, we did not demonstrate how the gap opens. That is the goal of this tutorial. We will replicate the plot from Topology in Condensed Matter course showing how the gap opens while on-site potential increases.

For this, the Bogoliubov transformation can be applied, which is a nifty tool in theoretical physics allowing us to find solutions for BCS superconducting systems like ours. Given the original form of the Kitaev chain Hamiltonian as presented earlier

H=−12μ∑jL(2aj†aj−1)−∑jL−1[w(aj†aj+1+aj+1†aj)−Δajaj+1−Δ∗aj+1†aj†)]\begin{aligned} H = -\frac{1}{2} \mu \sum_j^L (2 a_j^\dagger a_j - 1) - \sum_j^{L-1} [w (a_j^\dagger a_{j+1} + a_{j+1}^\dagger a_j) - \Delta a_j a_{j+1} - \Delta^\ast a_{j+1}^\dagger a_j^\dagger)] \end{aligned}

we may construct a mean-field approximation Bogoliubov-de Gennes Hamiltonian as follows

HBdG=∣0⟩⟨0∣⊗Hμ,w−∣1⟩⟨1∣⊗Hμ,w∗+∣0⟩⟨1∣⊗HΔ−∣1⟩⟨0∣⊗HΔ∗.H_\text{BdG} = \left \vert 0 \rangle \langle 0 \right \vert \otimes H_{\mu, w} - \left \vert 1 \rangle \langle 1 \right \vert \otimes H_{\mu, w}^\ast + \left \vert 0 \rangle \langle 1 \right \vert \otimes H_{\Delta} - \left \vert 1 \rangle \langle 0 \right \vert \otimes H_{\Delta}^\ast .

The HH has a Hilbert space of 2L2^L while HBdGH_\text{BdG} is much smaller of size 2L2L. The Hμ,wH_{\mu, w} is Hermitian and HΔH_{\Delta} is skew-symmetric. Both are of size 2L2L by 2L2L elements and constructed as follows.

Hμ,w=μ∑jL∣j⟩⟨j∣+w∑jL−1(∣j⟩⟨j+1∣+∣j+1⟩⟨j∣)HΔ=∑jL−1iΔ(∣j⟩⟨j+1∣−iΔ∗∣j+1⟩⟨j∣)\begin{aligned} H_{\mu, w} &= \mu \sum_j^L \left \vert j \rangle \langle j \right \vert + w \sum_j^{L-1} (\left \vert j \rangle \langle j+1 \right \vert + \left \vert j+1 \rangle \langle j \right \vert) \\ H_{\Delta} &= \sum_j^{L-1} i \Delta (\left \vert j \rangle \langle j+1 \right \vert - i \Delta^\ast \left \vert j+1 \rangle \langle j \right \vert) \end{aligned}

When we write H∗H^\ast we mean element-wise complex conjugation, not Hermitian conjugation. In Python the HBdGH_\text{BdG} Hamiltonian can be constructed as follows

def Hbdg(L, mu, w, delta):
    # sub-matrices, h-matrix
    MH = np.zeros((L, L), dtype=np.complex128)
    for j in range(L-1):
        MH[j, j] = mu
        MH[j, j+1] = np.conjugate(w)
        MH[j+1, j] = w
    MH[L-1, L-1] = mu

    # sub-matrices, D-matrix
    MD = np.zeros((L, L), dtype=np.complex128)
    for j in range(L-1):
        MD[j, j+1] = np.conjugate(1j*delta)
        MD[j+1, j] = 1j*delta

    # construct Hbdg matrix
    Hbdg = np.kron(np.array([[1, 0], [0, 0]]), MH)
    Hbdg += np.kron(np.array([[0, 0], [0, 1]]), -np.conjugate(MH))
    Hbdg += np.kron(np.array([[0, 1], [0, 0]]), MD)
    Hbdg += np.kron(np.array([[0, 0], [1, 0]]), -np.conjugate(MD))

    return Hbdg

and here below we apply it to study the system of L=20L = 20 sites increasing μ\mu up to value of 4w4 w where w=Δw = \Delta. The number of sites is impressive and would be numerically intensive if we wanted to simulate the whole system instead of applying the Bogoliubov-de Gennes approach.

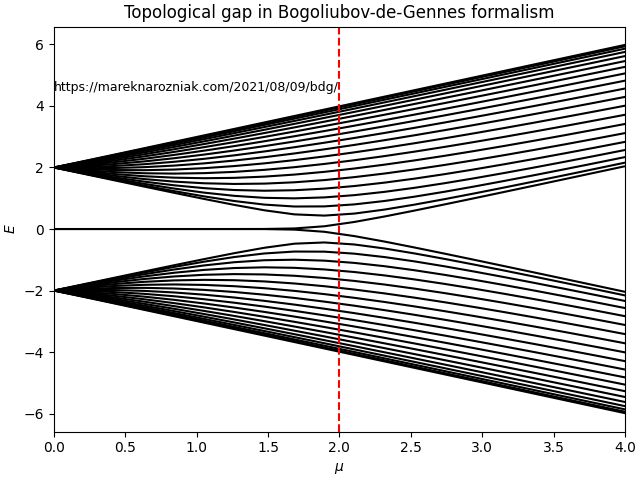
H_bdg spectrum of Kitaev Chain Hamiltonian

This matches the plot from Topology in Condensed Matter course nicely! We can observe the topological gap opening at μ=2w\mu = 2 w.

The energy spectrum obtained from HBdGH_\text{BdG} Hamiltonian is exact in the sense that in our case it provides energies of a single fermion in the 1D chain. From those energies of the multi-fermion system can be obtained by computing all binomial combinations of those energies. It is exact in the sense that it provides all the necessary information to recreate the full energy spectrum of the multi-fermion system.

The full source code of this simulation is published under an MIT license on GitHub. If you find errors please tweet me and let me know.

    [Back to Top]