Symmetric Ciphers
Share on:Cryptography is about writing secrets. From Ancient Greek κρυπτός (kryptós) means ‘hidden’ or ‘secret’, then γράφειν (graphein) means ‘to write’. Some of the related subjects such as Diffie-Hellman key exchange over eliptic curve, hashing functions and eliptic curve digital signature algorithm have already been covered on this blog. However, we haven’t yet explicitly written a secret message in protected way which was making this cryptography tutorial series less intuitive.
This gives us an excellent opportunity to introduce symmetric ciphers, which are the kind of ciphers that use same key for encryption and decryption. You can think of it in a way that there is no concept of public key, there is only private key. The message to be encrypted is called plaintext, private key that encrypts it is called cipher and once encrypted we call it ciphertext.
Simplest example I know is rotation cipher, such as ROT13 which is insecure and used mainly to hide spoilers on online boards. It consists of rotating the charset of domain size 26 by 13, which makes it an involutory function as ROT13(ROT13(X))=x. That’s how I chosen my robot name, ROT13(Marek)=Znerx is my robot name! You can check here the meaning of following spoiler: Inqre vf Yhxr'f sngure!. In case of ROT13 the private key is the number 13. The entire alphabet can be rotated by rot using a following function
def rotate(alphabet, rot):
return alphabet[rot:] + alphabet[:rot]
The ROT13 cipher is a particular case of Caesar’s cipher with private key, or shift value, fixed to 13. It does not make it much more secure as one might perform a frequency analysis of symbols and after a fair amount of trials guess the rotation number. We can make it slightly less insecure by introducing a key-word which is a specific word with unique letters that introduces a slight re-ordering in the charset. The key-word becomes the first letters of the charset and those letters are removed later on.
def applyCipher(alphabet, cipher):
unique = str(''.join(list(dict.fromkeys(list(cipher)))))
applied = str(alphabet)
for c in unique:
applied = applied.replace(c, '')
applied = unique + applied
return applied
Encryption function would then work as follows, it would rotate the key-worded alphabet and replace characters in the ciphertext by their rotated counterparts
def encrypt(plaintext, alphabet, cipher, rot):
lookup = rotate(applyCipher(alphabet, cipher), rot)
ciphertext = ''
for c in plaintext:
index = alphabet.index(c)
cp = lookup[index]
ciphertext += cp
return ciphertext
and decryption is same opration in reverse
def decrypt(ciphertext, alphabet, cipher, rot):
lookup = rotate(applyCipher(alphabet, cipher), rot)
plaintext = ''
for c in ciphertext:
index = lookup.index(c)
cp = alphabet[index]
plaintext += cp
return plaintext
I prepared two plaintexts and computed their ciphertexts for you as an example. But I only give you the first plaintext, its key-word is disappear and alphabet gets rotated by 7 characters. Do you recognize the song?
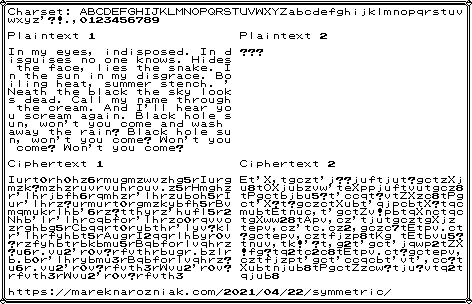
As for the second plaintext, I will keep it secret, but I give you the ciphertext and cipher is not strong so maybe if you have time and energy you could break it. The only hint I’ll give you is that is also a song!
If you are familiar with this blog you know I am in love with old 8-bit Pokémon aesthetics and I use them a lot in my tutorials. Started with figures in the vertex cover and independent set tutorial, quantum adiabatic optimization and constraint programming. I also use pokétext to write instagram blog. I decided it is about time to use pokétext to create a charset that can cover all single byte values and have my own raw bytes rendering module. I added math symbols and removed some graphics like borders, just to make it more usable for my purpose. So here it is

Now we can render raw byte strings in pokétext so it is time to try some more serious ciphers. My goal is to present to you the Rijndael, also known as Advanced Encryption Standards or simply AES since it has been announced as standard by NIST.
This is going to be a very top-down intro to AES because I did not implement it. For Diffie-Hellman key exchange over eliptic curve and eliptic curve digital signature algorithm we implemented those methods from scratch for purely educational purposes and I heard comments from some readers it is nice to see but also an overkill. So this time instead of visualizing steps of AES I will leave you with a reference and animation and instead of explaining it step by step I will show you something cool you can do with it.
The feature I find the most amazing is called hidden volumes. It makes is possible to concatenate ciphertexts one with another and hide encrypted data somewhere in the middle or at the end of the data block. This is effective because the plaintext is supposed to be padded with random data and ciphertext is indistinguishable from the random data. Let me show you what I mean. Below you can see a ciphertext I prepared.

The leftmost text is the ciphertext. You can’t tell where encrypted data is. In the middle you can see decrypted plaintext from this ciphertext after applying stakhanov cipher padded to 16 bits length and specific initial vector 6248a0359582697f1ad391525bebcfb0 (hexadecimal). It provides a decrypted message at the beginning. However, if instead of stakhanov we use d0om3rplyl1st cipher and different specific initial vector 8cc95298fdb22717f9710091ab74b1f5 from the same ciphertext we get a completely different message! This time at the end!
This has huge implications! You can carry around encrypted data with hidden volumes inside of it and if someone accuses you of having illegal secrets you can always provide a different ciphertext, one that decrypts the data you want them to see. You are in control. They can see only what you allow them to see.
I must say, there is one more hidden volume inside of the ciphertext, but I do not encourage you to break it. It is AES128 with CBC mode, pointless to even try. I used pycryptodome implementation. All the examples are included in the gist repository however for AES128 the decrypted output will be raw bytes as I have not yet decided if I want to make my pokétext renderer public or not.
How could that be used in practice? If you ever used grin-wallet for Grin cryptocurrency it has a function called init_secure_api. What it does it, first it runs a Diffie-Hellman key exchange over eliptic curve to establish a shared secret, then this shared secret is used as symmetric cipher between the two parties to encrypt the communication between the user and the wallet. This allows to use the wallet API in secure way even in insecure setup (such as lack of https protection).
Ciphers help us protect secrets. Hidden volumes help us protect the very existence of the secret. If you have some secrets to protect on your computer, do not handmade ciphers with Python, I recommend software like VeraCrypt to handle that for you.
It wouldn’t be my article if I didn’t make a cartoon-related anegdote, so here it comes. If the Sorceress knew about AES128 maybe she would not need He-Man to protect the secrets of Castle Grayskull from the Evil Forces of Skeletor. That would make the cartoon far less fun to watch. As usual, hope you enjoyed this short tutorial with few basic examples and feel free to tweet me if you find errors!
