Eliptic Curve Digital Signature Algorithm

It is not going to be the first time we will discuss the subject related to the eliptic curve over finite field. This time the subject of our discussion is going to be the idea of a digital signature, which will help us continue to build the foundations for even more advanced ideas. Previously we have discussed the Diffie-Hellman key exchange over eliptic curve which permits two parties, Alice and Bob, to come up with a shared secret over public channel without risking the potential eavesdropper to know the secret. Later, we introduced the aggrematon machine which also heavily, but indirectly relied on the eliptic curve. Along with the hashing functions we have complete foundations to start discussing the digital signatures.

Most of us associates the word signature with some sort of ink blob on the piece of paper. Digital signature is not quite the same idea but both do have at least one thing in common - the signing party has interacted with the signed document. If you have not yet seen the ecdh article it is highly recommended to get back to it and read it first as this article will not go in depth of many concepts introduced there. It is going to be assumed you are familiar with ideas such as private key, public key or hashing function.

Assuming we can just make a blob on the piece of paper, why do we even need a digital signature? The answer to that question can be found in the paper (Diffie & Hellman, 1976) by Diffie and Hellman themselves. Briefly, it is because the digital era has arrived. In simple terms what they meant was that the computers are sufficiently widely available and telecommunication channels are used often enough that the need for digital equivalent of a signature is a necessity. According to Diffie and Hellman, such signature in their own words

It must be easy for anyone to recognize the signature as authentic but impossible for anyone other than legitimate signer to produce.

The way such signature works is given some digital information, such as a file, it is possible to generate another digital information which is unique to that file and can only be produced by particular individual, for instance owner of a particular public key. Presence of such digital signature confirms that owner of the private key corresponding to the public key has generated a signature given this particular document.

Before we dive into the realm of the eliptic curves again and start signing documents like a congressman on coke, let us discuss the brief history of the idea. The eliptic curve digital signature (ECDSA) is not the first digital signature algorithm (DSA). Initially called a digital signature system (DSS) and proposed for the government use and standarized in (FIPS, 1994). As a response to that Vanstone proposed what we today call ECDSA (Vanstone, 1992). Vanstone proposed to adapt ElGamal signature scheme (Elgamal, 1985) to the ECC. At that time the idea of eliptic-curve has been well established by Koblitz and Miller (Koblitz, 1987; Miller, n.d.). I am not going to touch the subject of DSA at all because I am principally interested in eliptic curves. They are widely used today and this is not a history article.

The ECDSA digital signature is a tuple of integers

\left< s, x_R \right> \tag{I}

where $X_R$ is the $x$ -coordinate of the eliptic curve point $R = k G$ . Then $k$ is the random nonce and $s$ is the signature proof

s = k^{-1} e + d r \tag{II}

where $e$ is hashed message, $G$ the generator point and $d$ is the private key. As a quick reminder, the public key is $P = G d$ . The digital signature described above satisfies

s k = e + k G d \tag{III}

and can be verified by calculating

R^\prime = e s^{-1} G + r s^{-1} P \tag{IV}

and signature is valid if and only if

x_R = x_{R^\prime} \tag{V}

Now assuming the only way of computing $s$ is $(\text{II})$ then producing fake signature from the public key $p$ would require to solve the eliptic curve discrete logarithm problem (ECDLP). However it is not known if $(\text{II})$ is the only way of producing the signature proof, thus there is no formal proof difficulty of breaking ECDSA is equivalent of ECDLP. However, ECDSA has been used for decades extensively, including Bitcoin and Ethereum and there has been no incident of forging a signature to produce a fake transaction and stealing cryptographic coins. This provides an empirical evidence of security of ECDSA. To formally prove the security of ECDSA a different approach has been taken by Fersch (Fersch, Kiltz, & Poettering, 2016) based on bijective random oracle model. I am not an expert on it and I will just let you be the judges in this matter.

Another thing to mention is that $k$ does not necessarily need to be random, it could be deterministically chosen based on the $e$ value and the private key as specified in RFC6979. That would be the deterministic-ECDSA variant.

Now let us prepare a little example demonstrating this concept. We are going to re-use most of the code from Diffie-Hellman key exchange over eliptic curve article with same size of the finite fields. We are also going to design an extremely insecure hash function which yields a hash which is an integer that in range of that finite fields size $p = 13$ . For this to work we need the field order to be also a prime number, if we choose a curve $a = 1$ , $b = 7$ that will be the case.

def add_digits(num, p):
    return (num - 1) % p if num > 0 else 0

def hashtard(m, p):
    hash = hashlib.sha256(str.encode(m))
    num = int.from_bytes(hash.digest(), 'big')
    num = add_digits(num, p)
    return num

The hashing function above is extremely insecure as it easily leads to collisions. Our example is meant to be small so the hash values need to fit in the size of the finite field $\mathbb{F}_p$ . To know more about security of hashing functions please check the hashing functions tutorial.

We will be using the minicurve library for implementing and visualizing this signature.

from minicurve import MiniCurve as mc
from minicurve.helpers import inverse

A function that produces the signature based on $\text{II}$ is

def sign(e, k, d, P, p):
    Q = k*P
    s = np.mod(inverse(k, p)*(e + d*Q.x), p)
    return s, Q.x

and of course we also need a method for verifying the signatures

def verify(e, s, r, G, P, p):
    Q1 = np.mod(e*inverse(s, p), p)*G
    Q2 = np.mod(r*inverse(s, p), p)*P
    R = Q1+Q2
    if R.x == r:
        return True, R.x
    return False, R.x

Imagine Alice and Bob are friends for a long time, they know each others public keys (as all close friends do!). Their public (and private) keys are visualized as follows in the finite field $\mathbb{F}_p$ with $p = 13$

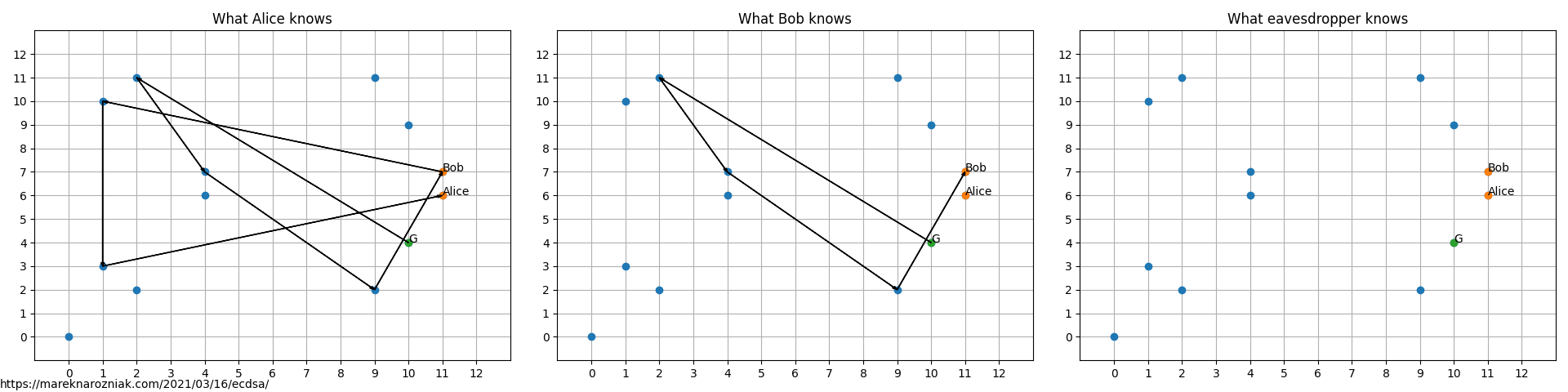
visualization of public and private keys for the ECDSA signature from perspective of each of the participants

As indicated, everyone knows own private key (visualized as arrow path in the $\mathbb{F}_p$ ) and everyone else’s public keys which are points in $\mathbb{F}_p$ . Even the random eavesdropper knows the public keys!

One morning Alice wakes up and finds two letters from Bob. The first one with very disturbing content

Dear Alice,

I am not sure where I am. It seems to be some kind of prison or a labor camp. I managed to convince someone to sneak out and send this letter to you. Please please please try to find me.

Miss you,
Bob
Signature: <10, 4>

while the other one was not disturbing but strange, nothing like the Bob she remembers

Dear Alice,

I am currently taking long holidays in a beautiful place. The food is delicious here. I spend most of my time having fun with new friends. The means of communications are not perfect here so I do not send you my address. Please do not try to reach me, I will message you first.

All the best,
Bob
Signature: <4, 5>

Fortunately each of the letters is accompanied with the ECDSA signature and Alice still has Bob’s public key from the old days. She decided to check both of the signatures $x_{R^\prime}$ and compare it with $x_R$ values. Alice computes the hash of both messages using e=hashtard(message, p) and then runs verify(e, s, r, G, P, p), the output she finds is astonishing

Bob's signature on message 1 is valid? True
Bob's signature on message 2 is valid? False

it seems like poor Bob is in trouble! Let’s hope she will manage to arrange an appropriate rescue mission for him. The signatures can be visualized as follows

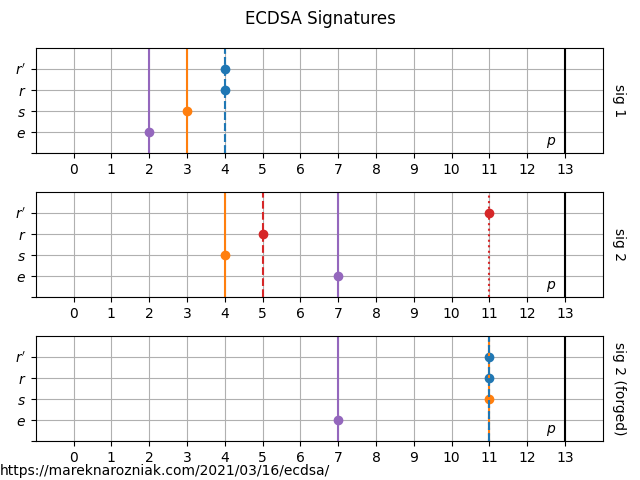
visualization of the ECDSA signatures as a series of 1D plots

where we recognize the valid signature by $x_R = r = r^\prime = x_{R^\prime}$ on the horizontal line. The third signature is an example of forged signature which was generated after brute-forcing the Bob’s private key. This is easily doable for such a small finite field.

The small size of the finite field $\mathbb{F}_p$ is very problematic. The hash function is not collision resistant and Bob’s kidnappers could just sit during coffee break and produce a letter that would eventually match one of older signatures. Another problem is the random nonce $k$ , as you may have noticed it is not randomly generated but set explicitly in sign(e, k, d, G, p). The reason for that is this number needs to admit a modular inverse and for small numbers it might often occur to violate condition of greatest common divisor being equal to $1$ .

Such a digital signature has a wide range of applications. It makes it possible to confirm the message is approved by the owner of particular public key. One of the examples where it comes to use is processing the Bitcoin transactions, miners would not append transaction to the block if the digital signature would not match. It is a part of their consensus algorithm in which wallet address is in fact a public key.

This is a toy example meant to be easy to visualize. To play more with such examples I recommend trying out the mini_ecdsa which is way more nicely written than my ECC code. I would like to thank @qubd, the author of mini_ecdsa for an interesting discussion regarding generating valid signatures over small finite field. His library has been extremely helpful to me as I was using it as a reference to compare and debug the output values of mine. I would also like to recommend a talk on digital signatures by Elichai Turkel which may inspire you to go beyond ECDSA and try Schnorr signatures instead! There also is a resource which I usually recommend, the tutorial on ECDSA in the Practical Cryptography for Developers book. If you are interested in running the code of this exact implementation please check this public gist repository for the complete source code!

That’s it for this tutorial, if you find errors or have some suggestions for improvements do not hesitate to tweet me!

Diffie, W., & Hellman, M. (1976). New directions in cryptography. IEEE Transactions on Information Theory, 22(6), 644–654. 10.1109/tit.1976.1055638
FIPS, P. U. B. (1994). 186 National Institute of Standards and Technology. FIPS PUB 186: Digital Signature Standard.
Vanstone, S. (1992). Responses to NIST’s proposal. Communications of the ACM, 35(7), 50–52.
Elgamal, T. (1985). A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Transactions on Information Theory, 31(4), 469–472. 10.1109/tit.1985.1057074
Koblitz, N. (1987). Elliptic curve cryptosystems. Mathematics of Computation, 48(177), 203–203. 10.1090/s0025-5718-1987-0866109-5
Miller, V. S. Use of Elliptic Curves in Cryptography. In Lecture Notes in Computer Science (pp. 417–426). Springer Berlin Heidelberg. 10.1007/3-540-39799-x_31
Fersch, M., Kiltz, E., & Poettering, B. (2016). On the Provable Security of (EC)DSA Signatures. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. ACM. 10.1145/2976749.2978413

[Back to Top]