Schnorr Signature

It is not the first time digital signatures appear on this blog as we have already introduced the ECDSA signatures earlier, as well as a more general introduction to the elliptic curve cryptography, which has been provided in the Diffie-Hellman key exchange over elliptic curve tutorial.

To be honest, I was planning to write about something completely different but it was so heavily reliant on the Schnorr signature which is at the same time sufficiently different from ECDSA to deserve its blog post. The concept I was going to write about will remain a surprise at the moment. If you read it in the future you might want to check what happened next and find it immediately.

As you might have already seen in the ECDSA signatures tutorial, the digital signature permits to prove a message has been seen by a person owning a particular private-public key pair. The example we provided in that particular tutorial consisted of a mysterious message from a friend and a digital signature helped estimate which of the messages is more likely to be true.

In this tutorial we will do something similar, we will use a different kind of signature and we will produce a multi-signature, which is a signature produced by multiple individuals. The Schnorr signatures (Schnorr, n.d.) have been known before ECDSA signatures, yet they were not so widely used due to the patent which expired in the year 2008. One of the advantages is the existence of proof that breaking the Schnorr signature is equivalent to breaking the discrete logarithm problem. Another one is the linear nature of the sign making it possible to easily combine multiple signatures.

Let us break the convention and denote the private key as $d$ , generator point we can keep as $G$ . Public key is thus

\begin{aligned} P = d G \end{aligned}

and additionally, we find a random integer $k$ which must fit within the prime order of the group generated by $G$ and we produce a point on the curve as follows

\begin{aligned} R = k G \end{aligned}

then we calculate

\begin{aligned} s = k - H(m \vert\vert P) d \end{aligned}

where $m$ is the signed message and $\vert\vert$ denotes concatenation and $H()$ is the hash function as those explained in our hashing functions tutorial. The signature is a tuple

\begin{aligned} \left< s, R \right> \tag{I} \end{aligned}

To verify the signature we proceed as follows. Given $\left< s, R \right>$ and message $m$ we have to check if

\begin{aligned} s G = R + H(m \vert\vert P) P \end{aligned}

We will be using the minicurve library for implementing and visualizing this signature.

from minicurve import MiniCurve as mc
from minicurve.helpers import inverse

The signature method is

def sign(m, k, d, G, p):
    # calculate public key R = k*G
    R = k*G
    # calculate e = H(M || r) where || is concatenation
    e = hashtard(m, p)
    # calculate the signature
    s = np.mod(k + d*e, p)
    # signature is s, R
    return s, R

where $k$ is the random nonce, $p$ is the order of the entire finite field. We also the verification method

def verify(m, s, G, P, R, p):
    # e_v = H(M || r_v)
    e = hashtard(m, p)
    # calculate the verification
    lhs = s*G
    rhs = R+e*P
    # test if lhs = rhs
    if lhs == rhs:
        return True, lhs, rhs
    return False, lhs, rhs

The implementation is confusing, please refer to previous ECC tutorials for more details.

Now to produce multi-signature we start by combining the keys of each of the participants using curve point addition

\begin{aligned} P_c = P_A + P_B \end{aligned}

then each of the participant is producing the signature, this should give us $\left< s_A, R_A \right>$ and $\left< s_B, R_B \right>$ for Bob. The $s_A$ and $s_B$ can be combined using modulo integer addition and for random points we use eliptic curve addition

\begin{aligned} s_c &= s_A + s_B \mod p \\ R_c &= R_A + R_B \end{aligned}

which gives as a multi-signature $\left< s_c, R_c \right>$ . This signature is verifiable only for the composite key $P_c$ , for the individual keys of Alice and Bob it is not valid.

As usual, let us perform a little demo. Let us imagine a scenario in which a very important message needs to be signed by both Alice and Bob. The message goes as follows

I say we take off and nuke the entire site from orbit. It's the only way to be sure.

Private keys of Alice and Bob are respectively $3$ and $5$ . Very insecure and small numbers, as they must fit in the range of prime order of group resulting from the generating point. Keys can be visualized as follows.

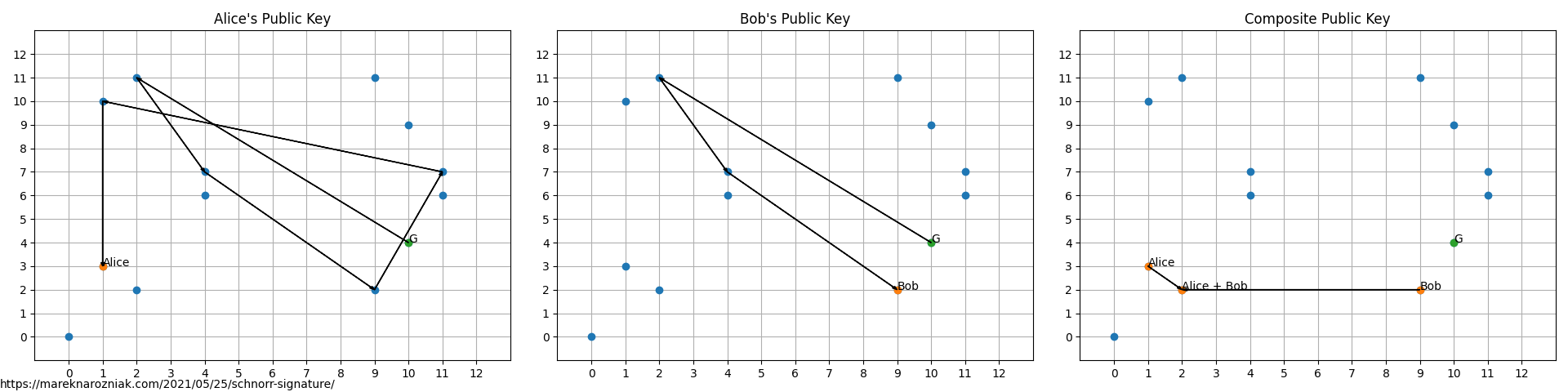
then their respective random nonces are $3$ and $5$ . Along with the ready signatures and both sides of the verification equation

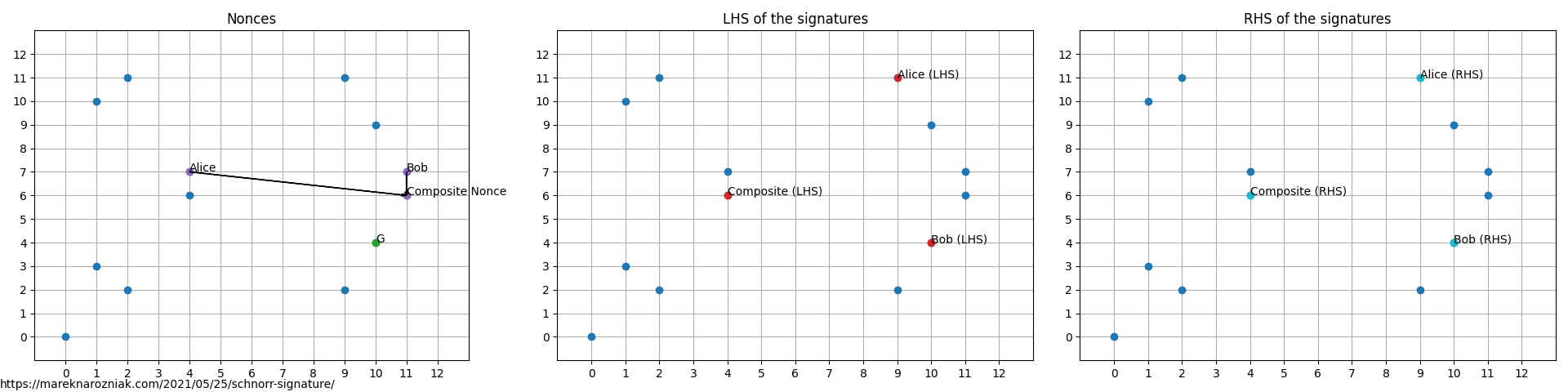
and we can observe that for all cases left-hand side equals the right-hand side indicating signatures validity.

If you run the source code of this example you will see the outputs confirming the validity of the result

Trying to verify the signature with just Alice's public key
failed
Trying to verify the signature with just Bob's public key
failed
Trying to verify the signature with the composite public key
valid

This was a short tutorial, but I hope it will end up useful as once we have Schnorr signatures and multi-signatures we can go into more advanced concepts, such as Pedersen commitments, confidential transactions, adaptor signatures, and much more!

If you like to know more, I based this tutorial on what the heck is Schnorr medium article and cryptography fandom Schnorr signature page.

I would like to thank John Tromp for answering my questions and providing comments regarding Schnorr’s signatures on the cryptography channel in the grincoin keybase team. I also thank vegycslol for a discussion that helped improve the quality of this tutorial and make it a lot less confusing.

If you find typos or errors in this text please do not hesitate to let me know, for which best way is to simply tweet me.

Schnorr, C. P. Efficient Identification and Signatures for Smart Cards. In Advances in Cryptology — CRYPTO’ 89 Proceedings (pp. 239–252). Springer New York. 10.1007/0-387-34805-0_22

[Back to Top]